The next problem on our area of a semi-circle worksheet we're going to talk about how to find the area of a semi-circle with diameter. We know that the area of a semi-circle is pi times the radius squared and then divided by 2. To get the radius all you do is you take the diameter divide by 2. So 3 divided by 2 is 1.5 feet so now we know the radius is 1.5 and then you follow the same procedure that you did in the previous problem. You take the radius which is 1.5 and you substitute it in where r used to be. Area is equal to pi times the radius which is 1.5 squared and then you're going to divide it by 2.
You do 1.5 times 1.5 which is 2.25 then you're going to do pi times 2.25 and that will give you 7.07 divided by 2 and your final answer will be 3.53 feet squared. The only extra step in finding the area of a circle with the diameter is having to divide the diameter by 2 to get the radius. Let's jump to number one on our area of a semicircle worksheet. In this case we are given the distance from the middle of the circle to the outer edge which is known as the radius. We know that the radius is equal to 6 inches because it's given to us in order to solve using the formula.
We're going to take our radius which is 6 inches and substitute it in for r into the formula. We take area equals pi times the radius which in this case is 6 squared and then divided by 2. First thing we do according to order of operations is 6 squared so 6 times 6 which is 36 and then we're going to divide by 2. The Area of a Semicircle is all of the area that is inside of a semicircle.
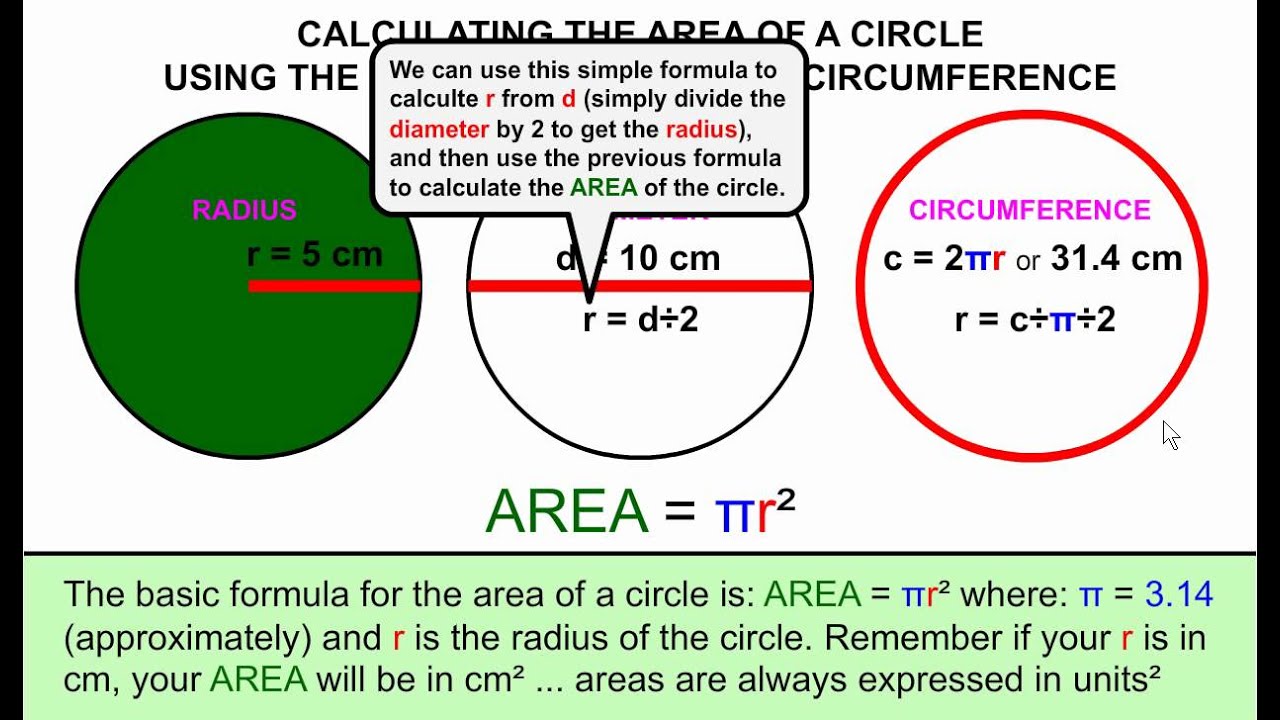
The way you find the Area of a Semicircle is similar to how you find the area of a circle. Usually you find the area of a semicircle using radius but sometimes you will have to find the Area of a Semicircle with diameter. The diameter is twice as long as the radius, or the radius is half of the diameter.
The formula for how to find Area of a Semicircle is area equals pi times the radius squared then divided by two. If you have the area of a semicircle with diameter that means that you have to divide the diameter by two to get the radius. Once you have the radius you can use the Area of a Circle formula. When simplifying you need to do follow the order of operations. You must square the radius and then multiply it times pi and then finally divide by two. The Area of a Semicircle is the area that is within a semicircle.
Typically you discover the area of a semicircle by utilizing the radius of the semicircle, however you can discover the Area of a Semicircle with diameter. The diameter is twice the length of the radius, in other words, the radius is half of the diameter. The equation for how to discover Area of a Semicircle is pi times the radius squared divided by two equals the area. In the event that you have to find the Area of a Semicircle with diameter you have to divide the diameter by two.
Then you can utilize the Area of a Semicircle equation. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. But first we need to review the formulas used to find the areas of rectangles and circles. If the area of the circle is not equal to that of the triangle, then it must be either greater or less.
We eliminate each of these by contradiction, leaving equality as the only possibility. Measure the Radius The next step is to measure or calculate the radius. For this example, we are going to assume the diameter of the semi-circle is given at 2 meters .
To find the radius we must divide the diameter by 2. This yields a result of 1 meter for the radius. Term Definition Area Area is the space within the perimeter of a two-dimensional figure.
Circle A circle is the set of all points at a specific distance from a given point in two dimensions. Diameter Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius.
For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information. Using these sheets will help your child to find the perimeter of a range of shapes including rectangles, rectilinear shapes, circles, quadrilaterals and regular shapes. Hi, and welcome to this video about finding the area of composite shapes made of rectangles and semicircles. The area of a regular polygon is half its perimeter times the apothem.
As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius. This tutorial gives you the semicircle radius formula and explains how to calculate the radius of the semicircle given the circumference or the diameter.
We use the circle formula to calculate the area, diameter, and circumference of a circle. The length between any point on the circle and its center is known as its radius. As can be seen in Definition of a Hexagon, each side of a regular hexagon is equal to the distance from the center to any vertex. This construction simply sets the compass width to that radius, and then steps that length off around the circle to create the six vertices of the hexagon. It looks like a straight line with a circular arc connecting its ends to one another. The straight edge of the semicircle is the diameter and the arc is half the circumference of a full circle with the same diameter.
You can find the radius of a semicircle using the formulas for circumference and diameter. Which formula you use will depend on what information you have been given to start. To find the area of a semicircle with diameter, divide the diameter by 2 to find the radius, and then apply the area of a semicircle formula. The area of the circle is the measure of the space or region enclosed inside the circle. In simple words, the area of a circle is the total number of square units inside that circle. We usually measure angles in degrees, for example, 90° in a right-angle, or 360° is a full revolution.
This is mainly for historical reasons — the Babylonians used a base-60 number system and for example we still use 60 minutes in a degree. Radian measure is crucial in later work on calculus. The idea is to define an angle so its size is the same as the size of the arc subtends it at the centre in a circle of unit radius. An alternative system is to measure angles in radians. Is made up of a large number of concentric circular pieces of very thin string.
The area of our semicircle is \(50\) pi meters squared. It's just the area of the rectangle plus the area of the semicircle. In truth, we don't really need the formula. Logic dictates that we're going to add the pieces of this composite shape to get our total area anyway. Find the equation of the circle with centre $(0;5)$ and radius $5$ ...
Find the equation of the circle with centre $(-5;-3)$ and radius $\sqrt$ ... In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. The area of a semicircle is half the area of the circle from which it is made. Any diameter of a circle cuts it into two equal semicircles.
The circles radius is simply half the diameter of the circle. Therefore, the radius of the semicircle is equal to the radius of the circle. An inscribed angle is usually formed in a circle with the help of two chords that tend to have a common endpoint on that circle.
The measure of this type of an angle is always half the measure of the intercepted arc. And according to the Inscribed Angle Theorem, an angle inscribed within a semicircle tends to be 90°, i.e., it's a right angle. This is due to the fact that the intercepted arc tends to measure 180°. So, naturally, any angle that is corresponding to it and is inscribed within, would measure half of it, which makes it a right angle. In the below figure, the line AC is called the diameter of the circle. The diameter divides the circle into two halves such that they are equal in area.
These two halves are referred to as the semicircles. The area of a semicircle is half of the area of a circle. The angle inscribed in a semicircle is always 90°.
The inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. It doesn't matter which point on the length of the arc, the angle created where your two lines meet the arc will always be 90°. The area of a semicircle is always expressed in square units, based on the units used for the radius of a circle. Here, we have discussed the programs to find the area and perimeter of semicircle in C, C++, Java, C#, PHP, python, and JavaScript. Hope you find the article helpful and informative.
When a line passes through the center and touches the two ends of the circle, then a semicircle is formed. The diameter of a circle divides it into two halves that are referred to as semicircles. In this article, we will discuss the program to find the area and perimeter of semicircle in different programming languages. Calculate the Area The final step is the plug all of the information into the formula or simply use the calculator.
Using the formula we find the area of this semi-circle is 1.570 meters squared. A figure consisting of a rectangle of length 8 cm and width 7 cm and two quarter-circles of radius 7 cm is cut from a piece of cardboard. Knowledge of area and perimeter of squares, rectangles, triangles and composite figures.
That means that we can find the radius by simply dividing our diameter by \(2\). Here the width, or the diameter, is \(73\) meters, so our radius is \(36.5\) meters. Now we just need to find the length of the rectangle.
Use this circle calculator to find the area, circumference, radius or diameter of a circle. Given any one variable A, C, r or d of a circle you can calculate the other three unknowns. We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle. This is called Tarski's circle-squaring problem.
How To Find Area Of Semicircle With Radius The nature of Laczkovich's proof is such that it proves the existence of such a partition but does not exhibit any particular partition. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well. How to Find the Area of a SemicircleTo find the area of a semi-circle, you need to know the formula for the area of a circle. This is because, a semi-circle is just the half of a circle and hence the area of a semi-circle is the area of a circle divided by 2.
The area of a semi-circle with radius r, is (πr2)/2. Π is a constant which is approximately 3.14 or 22/7. There is an actual sculpture based on the mechanism/concept of an arbelos in Kaatsheuvel, in the Netherlands.
The shape of a semicircle will be obtained by cutting a circle along its diameter and the full arc of a semicircle always measures 180 degrees. Example of a semicircular shape is protractor. The tool works as semicircle perimeter calculator as well - e.g., if you want to braid the rug, you can calculate how much lace you'll need. In our case, the perimeter equals 10.28 ft. The two endpoints of the semicircle's diameter and the inscribed angle will always form a right triangle inside the semicircle.
The perimeter of a semicircle is half the original circle's circumference, C, plus the diameter, d. Since the semicircle includes a straight side, its diameter, we cannot describe the distance around the shape as the circumference of a semicircle; it is a perimeter. The area of a semicircle is the space contained by the circle. The area is the number of square units enclosed by the sides of the shape.
Remember to state your answer in units squared. Since you're finding the area of a shape, you'll have to use units square d in your answer to indicate that you're working with a two-dimensional object. The bottom semi circle (on $EF$) has an area of $ \pi \times \frac$. Let the big semicircle on $CD$ have a radius of $a$, the medium one on $EF$ be radius $b$.






















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.